Colles de mathématiques
Rendez-vous à la même heure
Sujet
Clément et Amélie se donnent rendez-vous devant une salle de concert entre 19h et 20h.
Leurs instants d'arrivée après 19h sont indépendants et assimilés à une loi uniforme sur
[0,1].
Chacun attend jusqu'à un quart d'heure que l'autre arrive, puis rentre dans la salle.
Quelle est la probabilité qu'ils entrent ensemble dans la salle de concert ?
Corrigé de l'exercice de maths: Couples de variables aléatoires
Correction
On note  la variable aléatoire "instant d'arrivée de Clément" et
la variable aléatoire "instant d'arrivée de Clément" et  la variable aléatoire "instant d'arrivée d'Amélie", on cherche la probabilité pour que
la variable aléatoire "instant d'arrivée d'Amélie", on cherche la probabilité pour que 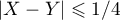 .
.
Méthode graphique:
 suit une loi uniforme sur le carré
suit une loi uniforme sur le carré ![$K=[0,1]\times[0,1]$](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/5.png) .
La probabilité recherchée est donc
.
La probabilité recherchée est donc
![\[P\lp\left|X-Y\right|\leqslant1/4\right)
=\dfrac{\textrm{aire}\lp\Bigl\{(x,y)\in K;\ |x-y|\leqslant1/4\Bigr\}\right)}{\text{aire}(K)}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/6.png)
On a .
.
Ainsi, et
et 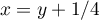 , et le domaine concerné:
, et le domaine concerné:
(0,0)(.25,0)(1,.75)(1,1)(.75,1)
\psline{->}(-.2,0)(1.2,0)
\psline{->}(0,-.2)(0,1.2)
\rput(1,-.1){1}
\rput(-.05,1){1}
\rput(-.05,.25){$\frac14$}
\rput(.25,-.1){$\frac14$}
\rput(-.05,-.1){0}
\psplot{0}{.75}{x .25 add}
\psplot{.25}{1}{x .25 sub}
\psline(1,0)(1,1)(0,1)
\rput(-.05,.75){$\frac34$}\psline[linestyle=dashed](0,.75)(1,.75)
\rput(.75,-.1){$\frac34$}\psline[linestyle=dashed](.75,0)(.75,1)
\end{pspicture}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/16.png)
L'aire du carré  vaut 1.
vaut 1.
L'aire de chaque triangle rectangle au dessous et au dessus du domaine est
![\[\dfrac12\tm\dfrac34\tm\dfrac34=\dfrac9{32}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/18.png)
et alors, l'aire, et la probabilité, recherchées sont donc
![\[p=1-2\tm\dfrac9{32}=\dfrac{14}{32}=\dfrac7{16}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/19.png)
Méthode analytique
On rappelle de plus que la densité d'une variable aléatoire uniforme sur![$[0;1]$](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/20.png) est
est
![\[f(x)=\la\begin{array}{ll}0 &\text{ si } x<0 \\
1 &\text{ si } 0<x<1\\
0 &\text{ si } x>1\enar\right.\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/21.png)
De même que dans la méthode précédente, on cherche la probabilité de l'événement
![\[\left|X-Y\right|<1/4\iff Y-1/4\leqslant X\leqslant Y+1/4\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/22.png)
Ainsi,
Au total, la probabilité recherchée est
![\[P\lp\left|X-Y\right|<1/4\right)
=\dfrac3{32}+\dfrac3{32}+\dfrac14=\dfrac{14}{32}=\dfrac7{16}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/38.png)
Méthode graphique:
![\[P\lp\left|X-Y\right|\leqslant1/4\right)
=\dfrac{\textrm{aire}\lp\Bigl\{(x,y)\in K;\ |x-y|\leqslant1/4\Bigr\}\right)}{\text{aire}(K)}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/6.png)
On a
Ainsi,
- pour
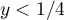 , on a donc
, on a donc 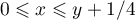
- pour
 , on a donc
, on a donc 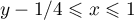
- pour
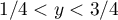 , on a
, on a 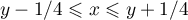 .
.
(0,0)(.25,0)(1,.75)(1,1)(.75,1)
\psline{->}(-.2,0)(1.2,0)
\psline{->}(0,-.2)(0,1.2)
\rput(1,-.1){1}
\rput(-.05,1){1}
\rput(-.05,.25){$\frac14$}
\rput(.25,-.1){$\frac14$}
\rput(-.05,-.1){0}
\psplot{0}{.75}{x .25 add}
\psplot{.25}{1}{x .25 sub}
\psline(1,0)(1,1)(0,1)
\rput(-.05,.75){$\frac34$}\psline[linestyle=dashed](0,.75)(1,.75)
\rput(.75,-.1){$\frac34$}\psline[linestyle=dashed](.75,0)(.75,1)
\end{pspicture}\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/16.png)
L'aire de chaque triangle rectangle au dessous et au dessus du domaine est
et alors, l'aire, et la probabilité, recherchées sont donc
Méthode analytique
On rappelle de plus que la densité d'une variable aléatoire uniforme sur
![\[f(x)=\la\begin{array}{ll}0 &\text{ si } x<0 \\
1 &\text{ si } 0<x<1\\
0 &\text{ si } x>1\enar\right.\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/21.png)
De même que dans la méthode précédente, on cherche la probabilité de l'événement
Ainsi,
- pour
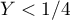 , on a donc
, on a donc 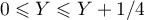
et on a alors la probabilité
![\[P\lp0\leqslant X<Y+1/4\rp=\dsp\int_0^{Y+1/4}1\,dx=Y+1/4\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/25.png)
et donc la probabilité pour tous les :
:
![\[\begin{array}{ll}
\dsp\int_0^{1/4}\left( y+1/4\rp\,dy
&=\Bigl[\dfrac12y^2+\dfrac14y\Bigr]_0^{1/4}\\[1.1em]
&\hspace{-3em}=\dfrac12\lp\dfrac14\rp^2+\dfrac14\tm\dfrac14=\dfrac3{32}
\enar\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/27.png)
- pour
 , on a donc
, on a donc 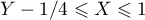
et on a alors la probabilité
![\[P\left( Y-1/4\leqslant X<1\rp=\dsp\int_{Y-1/4}^11\,dx=1-\left( Y-1/4\rp=-Y+5/4\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/30.png)
et donc la probabilité pour tous les :
:
![\[\begin{array}{ll}
\dsp\int_{3/4}^1\left( -y+5/4\rp\,dy
&=\Bigl[-\dfrac12y^2+\dfrac54y\Bigr]_{3/4}^1\\[1.2em]
&\hspace{-5em}=\lp-\dfrac12+\dfrac54\right)
-\lp-\dfrac12\lp\dfrac34\rp^2+\dfrac54\tm\dfrac34\rp
=\dfrac3{32}
\enar\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/32.png)
- Enfin, pour
 , on a
, on a 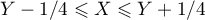 .
.
et on a la probabilité
![\[\int_{Y-1/4}{Y+1/4}1\,dx=\dfrac12\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/35.png)
et donc la probabilité pour tous les ,
,
![\[\int_{1/4}^{3/4}\dfrac12\,dy=\dfrac14\]](/Generateur-Devoirs/Colles/CVA/rdv-concert_c/37.png)
Au total, la probabilité recherchée est