🔍

Colles de mathématiques

Sous-espaces vectoriels supplémentaires dans R4


Sujet


On considère les vecteurs v1 = (1,0,0,1), v2 = (0,0,1,0), v3 = (0,1,0,0), v4 = (0,0,0,1) et v5 = (0,1,0,1) dans R4.
  1. Vect{v1, v2} et Vect{v3} sont-ils supplémentaires dans R4 ?
  2. Vect{v1, v2} et Vect{v4, v5} sont-ils supplémentaires dans R4 ?
  3. Vect{v1, v3, v4} et Vect{v2, v5} sont-ils supplémentaires dans R4 ?

Corrigé de l'exercice de maths: Espaces vectoriels

Correction


  1. En considérant les dimensions: dim(Vect{v1, v2})≤2 et dim(Vect{v3}) = 1 et 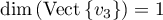$\dim\lp\text{Vect}\left\{v_3\right\}\rp=1$ et donc ces deux sous-espaces ne peuvent pas être supplémentaires dans R4 car dim(R4) = 4.

  2. Les dimensions peuvent ici concorder. On pose F = Vect{v1, v2} et G = Vect{v4, v5}.
    Pour montrer la somme directe, il faut montrer que l'intersection est réduite au vecteur nul: F∩G = {0}, et que F+G = R4.
    Soit donc u∈F∩G, alors il existe a et b tels que u = av1 + bv2 d'une part et il existe c et d tels que u = cv4 + dv5 d'autre part, soit aussi
    \[\begin{array}{lcl}&&u=av_1+bv_2=cv_4+d_v5\\[1em] &\iff& a\lp\begin{array}{c}1\\0\\0\\1\enar\right) +b\lp\begin{array}{c}0\\0\\1\\0\enar\right) =c\lp\begin{array}{c}0\\0\\0\\1\enar\right) +d\lp\begin{array}{c}0\\1\\0\\1\enar\rp\\[3em] &\iff&\la\begin{array}{ll} a=0\\ 0=d\\ b=0\\ a=c+d \enar\right.\iff a=b=c=d=0 \enar\]

    Ainsi, u = 0 et la somme de F et G est directe. Il reste à démontrer que cette somme est bien R4 (et non pas un sous-espace stricte de R4).
    On a F+G = Vect{v1, v2, v4, v5}. Soit u(x, y, z, t)∈R4, on cherche quatre coefficients a, b, c et d tels que u = av1 + bv2 + cv4 + dv5, soit
    \[\lp\begin{array}{c}x\\y\\z\\t\enar\rp= a\lp\begin{array}{c}1\\0\\0\\1\enar\right) +b\lp\begin{array}{c}0\\0\\1\\0\enar\right) +c\lp\begin{array}{c}0\\0\\0\\1\enar\right) +d\lp\begin{array}{c}0\\1\\0\\1\enar\rp\]

    ce qui est équivalent au système:
    \[\la\begin{array}{ll} x=a\\ y=d\\ z=b\\ t=a+c+d\enar\right. \iff \la\begin{array}{ll} a=x\\ b=z\\ c=t-a-d=t-x-y\\ d=y\enar\right.\]

    Ainsi, pour tout vecteur u(x, y, z, t) il existe une combinaison linéaire de F+G, ce qui montre que F+G = R4, et donc, avec le résultat précédent sur l'intersection, F⊕G = R4.

  3. Ces sous-espaces ne peuvent pas être supplémentaires car il y a trop de vecteurs. D'après la question précédente, on a bien la somme Vect{v1, v3, v4}+Vect{v2, v5} = R4 mais l'intersection n'est pas réduite au vecteur nul.