🔍

Colles de mathématiques

Sur les valeurs propres d'une matrice aléatoire

Oral HEC - filière B/L, 2022



Exercice de maths: Diagonalisation - Variables aléatoires continues - Annales HEC - B/L

Sujet


oral HEC, BL - 2022 - Exercice sans préparation.
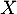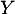Soit $X$ et $Y$ deux variables aléatoires indépendantes dfinies sur le même espace probabilisé 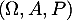$(\Omega, A, P)$, suivant la même loi géométrique de paramètre $p\in]0, 1[$.
Pour tout $\omega\in\Omega$, on pose
\[A(\omega)=\lp\begin{array}{cc}X(\omega)&Y(\omega)\\Y(\omega)&X(\omega)\enar\rp\]


  1. Déterminer la probabilité que 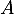$A$ soit inversible.
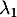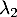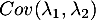  2. Soit $\lambda_1$ et $\lambda_2$ les variables aléatoires égales aux valeurs propres de $A$. Calculer $Cov(\lambda_1,\lambda_2)$.

Correction